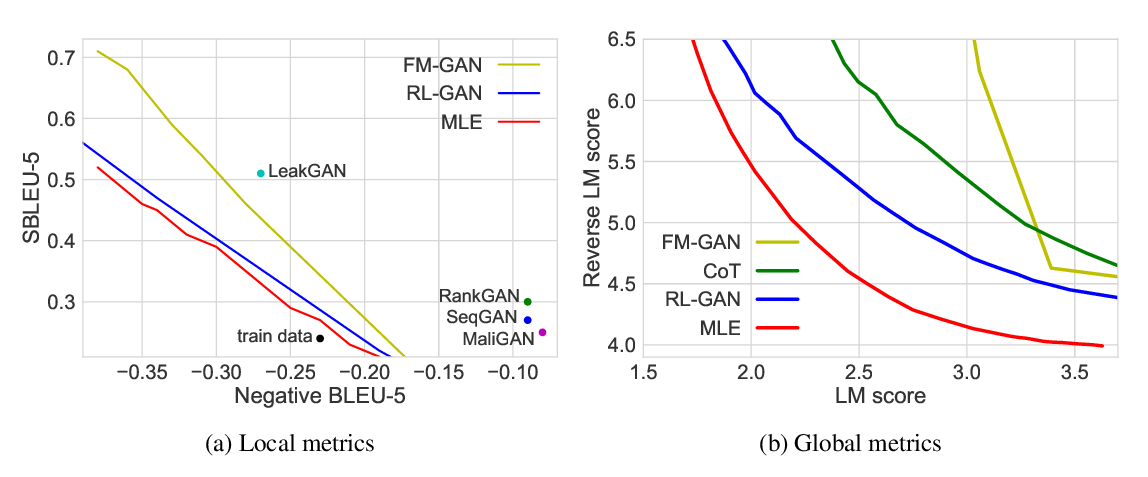
Abstract: For typical sequence prediction problems such as language generation, maximum likelihood estimation (MLE) has commonly been adopted as it encourages the predicted sequence most consistent with the ground-truth sequence to have the highest probability of occurring. However, MLE focuses on once-to-all matching between the predicted sequence and gold-standard, consequently treating all incorrect predictions as being equally incorrect. We refer to this drawback as {\it negative diversity ignorance} in this paper. Treating all incorrect predictions as equal unfairly downplays the nuance of these sequences' detailed token-wise structure. To counteract this, we augment the MLE loss by introducing an extra Kullback--Leibler divergence term derived by comparing a data-dependent Gaussian prior and the detailed training prediction. The proposed data-dependent Gaussian prior objective (D2GPo) is defined over a prior topological order of tokens and is poles apart from the data-independent Gaussian prior (L2 regularization) commonly adopted in smoothing the training of MLE. Experimental results show that the proposed method makes effective use of a more detailed prior in the data and has improved performance in typical language generation tasks, including supervised and unsupervised machine translation, text summarization, storytelling, and image captioning.