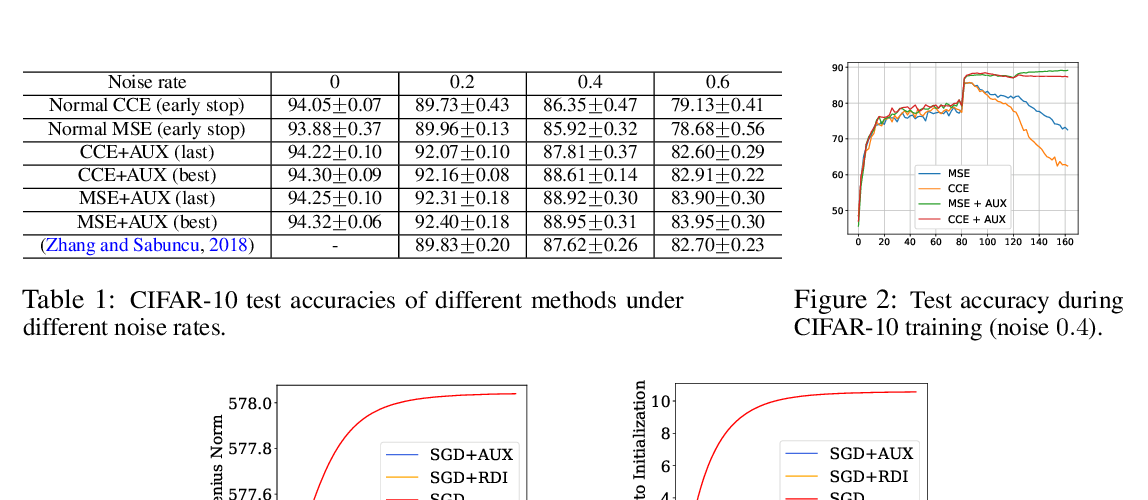
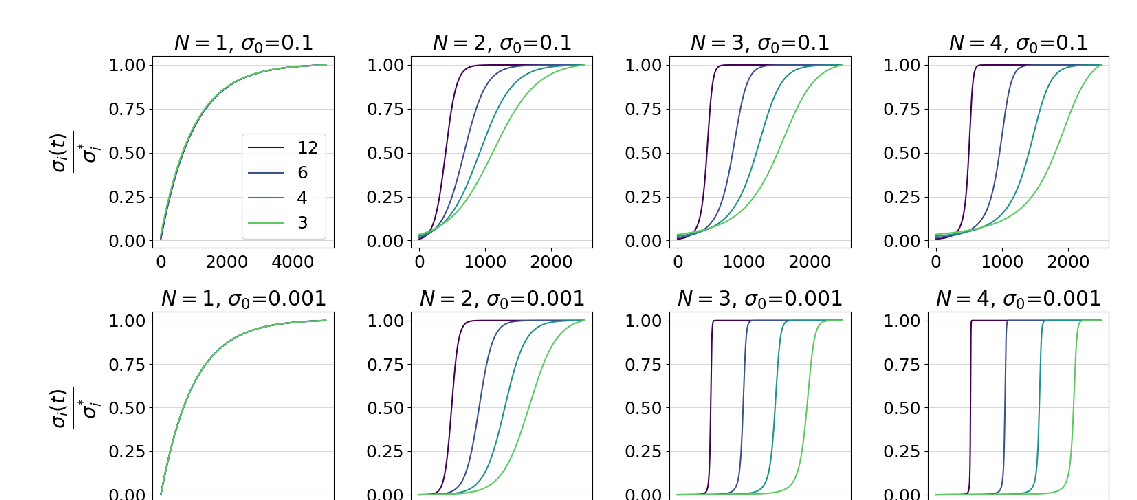
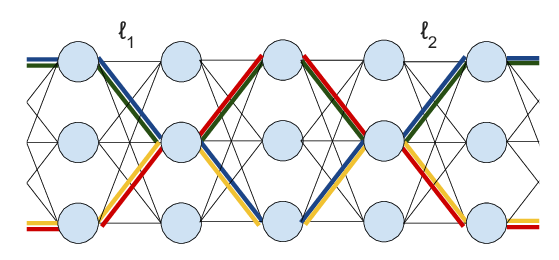
Abstract: Understanding the asymptotic behavior of wide networks is of considerable interest. In this work, we present a general method for analyzing this large width behavior. The method is an adaptation of Feynman diagrams, a standard tool for computing multivariate Gaussian integrals. We apply our method to study training dynamics, improving existing bounds and deriving new results on wide network evolution during stochastic gradient descent. Going beyond the strict large width limit, we present closed-form expressions for higher-order terms governing wide network training, and test these predictions empirically.