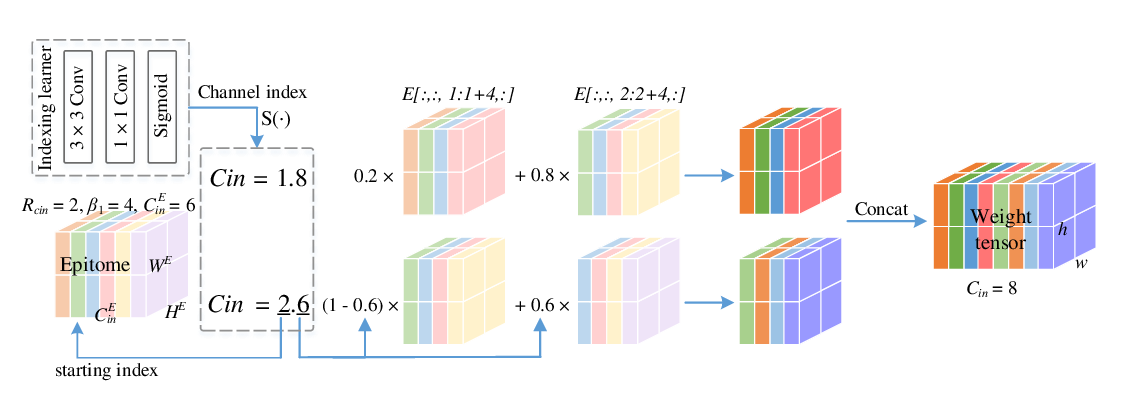
Abstract:
We present a novel method of compression of deep Convolutional Neural Networks (CNNs) by weight sharing through a new representation of convolutional filters. The proposed method reduces the number of parameters of each convolutional layer by learning a $1$D vector termed Filter Summary (FS). The convolutional filters are located in FS as overlapping $1$D segments, and nearby filters in FS share weights in their overlapping regions in a natural way. The resultant neural network based on such weight sharing scheme, termed Filter Summary CNNs or FSNet, has a FS in each convolution layer instead of a set of independent filters in the conventional convolution layer. FSNet has the same architecture as that of the baseline CNN to be compressed, and each convolution layer of FSNet has the same number of filters from FS as that of the basline CNN in the forward process. With compelling computational acceleration ratio, the parameter space of FSNet is much smaller than that of the baseline CNN. In addition, FSNet is quantization friendly. FSNet with weight quantization leads to even higher compression ratio without noticeable performance loss. We further propose Differentiable FSNet where the way filters share weights is learned in a differentiable and end-to-end manner. Experiments demonstrate the effectiveness of FSNet in compression of CNNs for computer vision tasks including image classification and object detection, and the effectiveness of DFSNet is evidenced by the task of Neural Architecture Search.