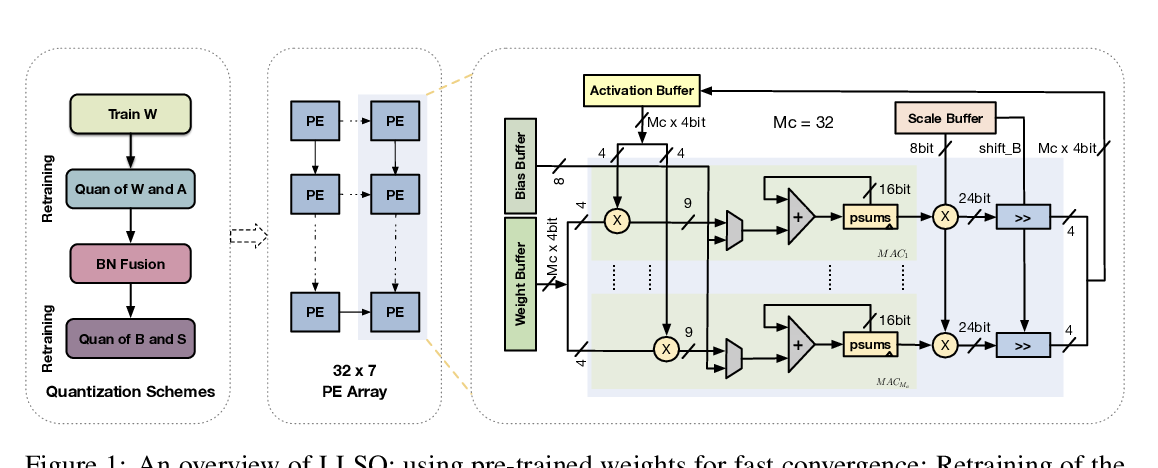
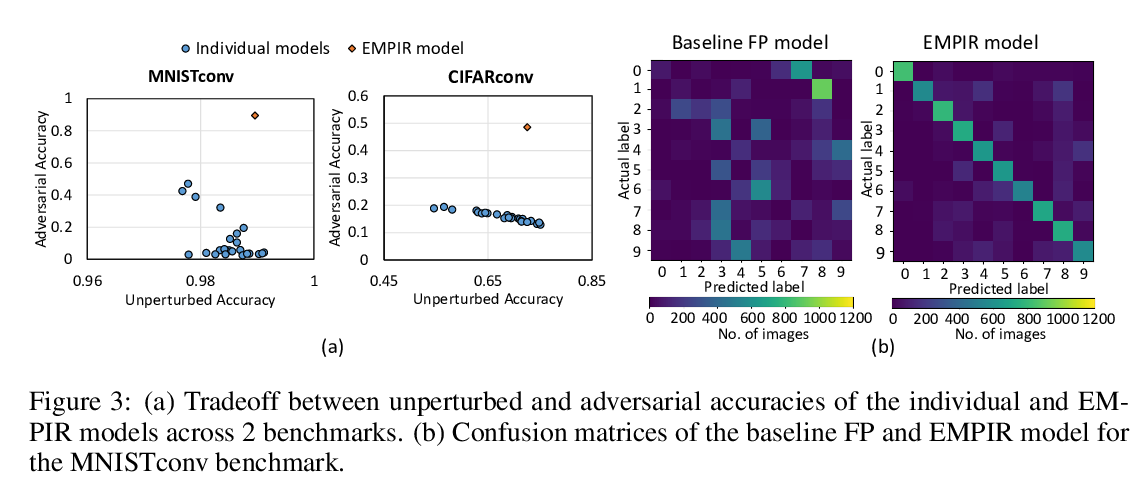
Abstract: Bayesian learning of model parameters in neural networks is important in scenarios where estimates with well-calibrated uncertainty are important. In this paper, we propose Bayesian quantized networks (BQNs), quantized neural networks (QNNs) for which we learn a posterior distribution over their discrete parameters. We provide a set of efficient algorithms for learning and prediction in BQNs without the need to sample from their parameters or activations, which not only allows for differentiable learning in quantized models but also reduces the variance in gradients estimation. We evaluate BQNs on MNIST, Fashion-MNIST and KMNIST classification datasets compared against bootstrap ensemble of QNNs (E-QNN). We demonstrate BQNs achieve both lower predictive errors and better-calibrated uncertainties than E-QNN (with less than 20% of the negative log-likelihood).