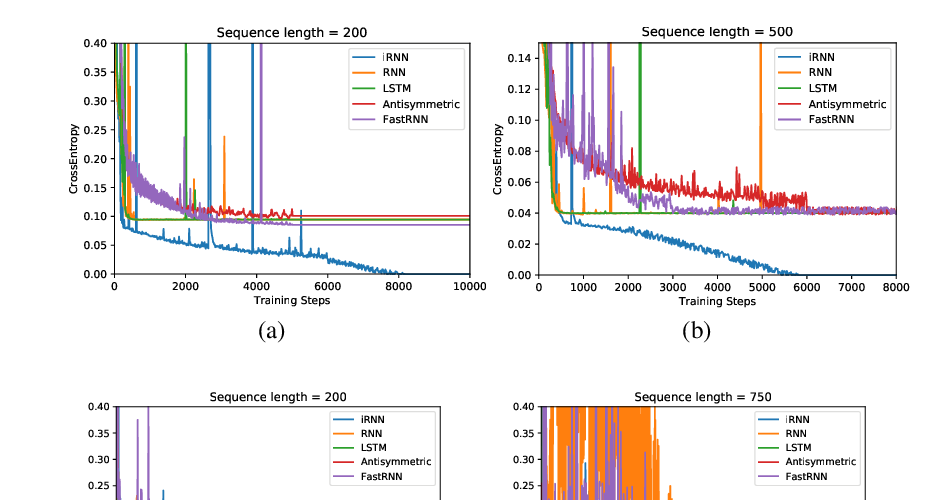
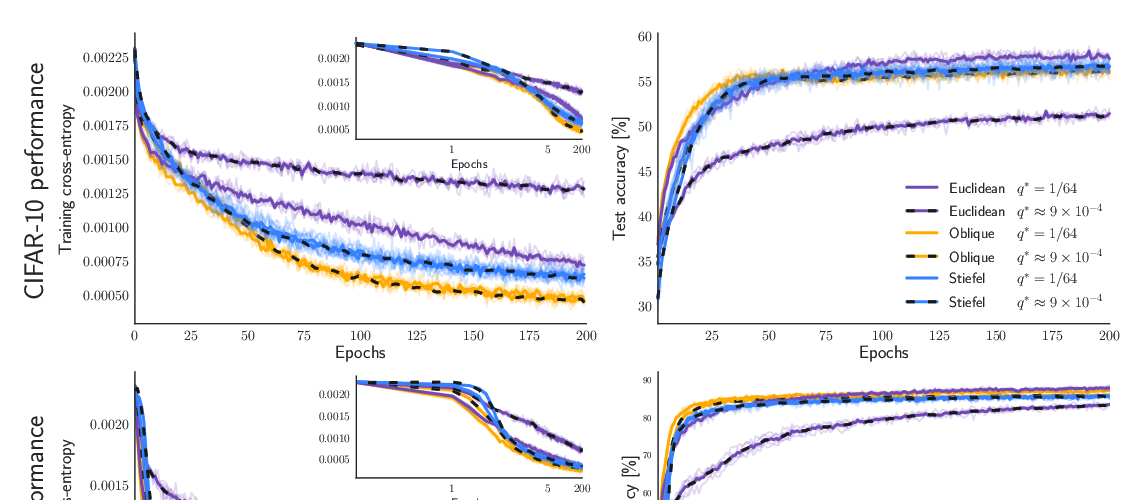
Abstract: Training recurrent neural networks (RNNs) is a hard problem due to degeneracies in the optimization landscape, a problem also known as vanishing/exploding gradients. Short of designing new RNN architectures, previous methods for dealing with this problem usually boil down to orthogonalization of the recurrent dynamics, either at initialization or during the entire training period. The basic motivation behind these methods is that orthogonal transformations are isometries of the Euclidean space, hence they preserve (Euclidean) norms and effectively deal with vanishing/exploding gradients. However, this ignores the crucial effects of non-linearity and noise. In the presence of a non-linearity, orthogonal transformations no longer preserve norms, suggesting that alternative transformations might be better suited to non-linear networks. Moreover, in the presence of noise, norm preservation itself ceases to be the ideal objective. A more sensible objective is maximizing the signal-to-noise ratio (SNR) of the propagated signal instead. Previous work has shown that in the linear case, recurrent networks that maximize the SNR display strongly non-normal, sequential dynamics and orthogonal networks are highly suboptimal by this measure. Motivated by this finding, here we investigate the potential of non-normal RNNs, i.e. RNNs with a non-normal recurrent connectivity matrix, in sequential processing tasks. Our experimental results show that non-normal RNNs outperform their orthogonal counterparts in a diverse range of benchmarks. We also find evidence for increased non-normality and hidden chain-like feedforward motifs in trained RNNs initialized with orthogonal recurrent connectivity matrices.